VERIFICA A COMPRESSIONE ASTE IN LEGNO
Il problema dell’instabilità dell’equilibrio risolto per pilastri in legno. Tale problema è risolto con il metodo di Eulero che imposta l’equilibrio in condizione deformata. Dopo aver valutato se l’asta è snella o tozza si riconduce lo studio ad una verifica di resistenza.
Nota la geometria del pilastro si ricava la snellezza λ nelle due direzioni ortogonali e la si confronta con la snellezza critica λcr.
Tale λcr è calcolata dal confronto tra la tensione critica σcr e la tensione massima sopportabile del pilastro soggetto a compressione fc,0,k.
Dove:
σcr = π2*E/λ2 = fc,0,k => λcr = π*(E0,k/fc,0,k)^(1/2)
In questo foglio di calcolo si valutano inizialmente le snellezze assolute che divise per il valore critico danno la snellezza relativa λrel.λy / λcr = λrel,y
λz / λcr = λrel,z
λrel,y ≤ 0.3 e λrel,z ≤ 0.3
allora il pilastro è tozzo e si procede con la verifica di compressione; se invece:λrel,y > 0.3 oppure λrel,z > 0.3
allora il pilastro è snello e si procede con la verifica di stabilità.Quindi si valutano i coefficienti kc,y e kc,y:
posto:
ky=0.5*(1+βc*(λrel,y-0.3)+λrel,y2);
kz=0.5*(1+βc*(λrel,z-0.3)+λrel,z2);
conβc=0.2 per legno massiccio
βc=0.1 per legno lamellare
risultano:kc,y = 1/(ky+((ky2-λrel,y2)^(1/2)));
kc,z = 1/(kz+((kz2-λrel,z2)^(1/2)));
Ovviamente se l'asta è tozza:kc,y = kc,z = 1;
La verifica risulta soddisfatta se:σc=N/A ≤ kc,y*fc,0,d
σc=N/A ≤ kc,z*fc,0,d
con:fc,0,d=kmod*fc,0,k/γm;
kmod=coefficiente minore o uguale all'unità che tiene conto della durata del carico e del livello di umidità del legno in funzione al tipo di esposizione a cui è sottoposto;
γm= coefficiente di sicurezza parziale del materiale:
γm=1.5 (legno massiccio)
γm=1.45 (legno lamellare)
CLASSI DI RESISTENZA
| Flessione | fm,k | |
| Trazione parallela | ft,0,k | |
| Trazione perpendicolare | ft,90,k | |
| Compressione parallela | fc,0,k | |
| Compressione perpendicolare | fc,90,k | |
| Taglio | fv,k | |
| Taglio per rotolamento (*) | fv,rol,k | |
| Modulo elastico parallelo medio | E0,mean | |
| Modulo elastico parallelo caratteristico | E0,k | |
| Modulo elastico perpendicolare medio | E90,mean | |
| Modulo elastico tangenziale medio | Gmean | |
| Modulo elastico tangenziale caratteristico (*) | Gk | |
| Modulo elastico tangenziale per rotolamento medio (*) | GR,mean | |
| Massa volumica caratteristica(5%) | ρk | |
| Massa volumica media | ρmean | |
(*) Questi valori non vengono dati nelle tabelle, ma sono calcolati assumendo:
|
||
CARATTERISTICHE DEL PILASTRO
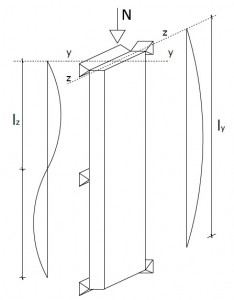
| Sezione circolare | |
| Sezione rettangolare |
| Base B (m) | ||
| Altezza H (m) | ||
| Diametro D (m) | ||
| Area della sezione A (m2) | ||
| Lunghezza L (m) | ||
| Esistenza del ritegno flessionale | ||
| Sforzo normale agente N (kN) | ||
| Fattore di sicurezza γm | ||
| Classe di durata e di servizio del carico | ||
| Kmod | ||







