CONFRONTO TRA MODELLI

In questo articolo si vogliono dimostrare le differenze che nascono nella modellizzazione, in campo elastico lineare, di un elemento “trave” ed il suo analogo bidimensionale: elemento “piastra ortotropa”, in modo da valutare se i risultati ottenuti nel calcolo semplificato con trave continua su appoggi fissi, siano almeno paragonabili a quelli ottenuti dalla modellazione più accurata fatta con elementi bidimensionali.
Naturalmente il risultato atteso non è quello di ottenere la perfetta coincidenza delle caratteristiche di sollecitazioni, bensì dimostrare che un approccio semplificato possa portare a risultati comparabili con l’analisi più sofisticata e comunque rispetto ad essa sempre di poco sovrastimata, come si suol dire fornendo risultati a “vantaggio di sicurezza”.
Per la verificasi confrontano una trave semplicemente appoggiata lunga 4m, realizzata con una sezione a “T” 20+5, ed un elemento bidimensionale di estensione 4m x 8m, appoggiato sui quattro lati e modellato con elementi “shell”, ossia elementi bidimensionali che descrivono il comportamento di lastra e piastra di Mindlin. La piastra ha la soletta alta 5cm e le nervature di larghezza 12cm con interasse a 50cm, per l’elemento si definisce un passo della mesh di 25cm.
Sulla piastra, ottenuta idealmente dall’unione di 16 travetti, si applica il carico di prova pari a 1 kN/m², distribuito sulla superficie delineata dalla soletta, mentre per la trave si applica un carico lineare pari a 0,5 kN/m, ottenuto dal prodotto del carico superficiale applicato per la piastra per la larghezza della base superiore della sezione di solaio: 50cm.
Per la trave in semplice appoggio il calcolo delle caratteristiche di sollecitazioni è immediato, il momento flettente è dato dalla nota relazione Pl2/8=1kNm, la sollecitazione tagliante vale Pl/2=1kN.
Si passa ora allo studio delle tensioni ricavate per la piastra attraverso un software agli elementi finiti “FEM”. Nella figura 1 e 2 sono riportate le mappe di tensione relative ai momenti flettenti nelle due direzioni principali del solaio, i travetti sono disposti secondo il lato corto della piastra.
La prima evidenzia come l’andamento sia chiaramente monodirezionale palesando un comportamento di trave appoggiata nella direzione dei travetti. Nell’immagine l’estesa zona blu rappresenta il momento positivo, massimo nel centro e progressivamente ridotto man mano che ci si avvicina al bordo. Si osserva come il comportamento monodirezionale sia disturbato ai bordi: destro e sinistro, questo perché il travetto esterno risente dell’influenza del vincolo esteso sul lato, che per questa analisi è stato collegato sull’ala superiore.
La seconda descrive sostanzialmente l’andamento del momento flettente nella direzione lunga della piastra, si nota quale sia l’effetto irrigidente dei travetti. Infatti ad esclusione delle zone laterali si analizza come la sollecitazione sia positiva tra un travetto e l’altro e negativa quando vi è in corrispondenza. Si nota che il modello descrive qualitativamente il comportamento di una trave continua su appoggi fissi, diretta nella dimensione lunga della piastra, in cui l’appoggio fisso è dato dalla nervatura.

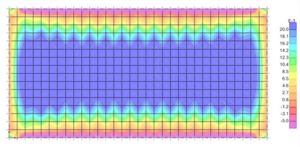
Figura 1: Momento di piastra in direzione longitudinale

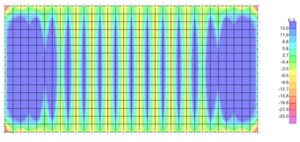
Figura 2: Momento di piastra in direzione trasversale

Nella figura 3 e 4 sono riportate le mappe di tensione relative alle sollecitazioni di taglio nelle due direzioni principali del solaio.
La prima immagine descrive la sollecitazione tagliante relativa alla direzione dei travetti, anche in questo caso è evidente il comportamento monodirezionale, in quanto la piastra risente principalmente degli appoggi in alto e in basso trasportando le tensioni dal centro verso gli estremi in modo uniforme.
La seconda descrive l’andamento del taglio nella direzione ortogonale alle nervature, anche per questa è evidente come il flusso delle tensioni sia diretto in modo unidirezionale dal centro verso i bordi laterali.
La sollecitazione tagliante è massimi sui bordi e si annulla in mezzeria in analogia all’andamento a farfalla della sollecitazione di taglio per la trave appoggiata, uniformemente caricata. Il comportamento appena descritto viene “disturbato” dai vincoli posizionati a destra e sinistra dell’elemento.

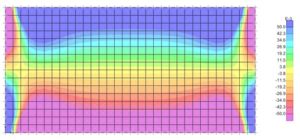
Figura 3: Taglio di piastra in direzione longitudinale

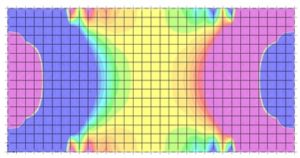
Figura 4: Taglio di piastra in direzione trasversale

Dalla scienza delle costruzioni è noto che i valori di tensione ricavati per i modelli bidimensionali sono forze su unità di lunghezza, dunque per effettuare il confronto con modelli monodimensionali occorre compiere delle integrazioni di tensione su determinate lunghezze.
Per il confronto le integrazioni sono state calcolate in punti specifici, ossia sui bordi in prossimità degli appoggi e in mezzeria, limitandosi all’estensione del travetto. L’analisi delle sezioni si conduce a partire dai travetti di bordo fino alla mezzeria con lo scopo di quantificare le sollecitazioni nella direzione delle nervature tralasciando quelle ortogonali.

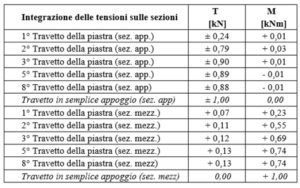
Appare evidente come il comportamento dei primi travetti sia influenzato dalla distribuzioni di vincoli laterali in quanto presentano sollecitazioni molto più basse di quelle calcolate con il modello semplificato di trave appoggiata, mentre a partire dal 3° travetto le sollecitazioni sono comparabili con quelle del modello monodimensionale fino ad ottenere la massima similarità per il travetto numero 8, cioè quello posizionato nella mezzeria.
È interessante notare come i valori ricavati non superano mai quelli ottenuti dal modello semplificato, questo accade perché la portanza dell’elemento bidimensionale virtualmente fa affidamento su due ordini di travi tra loro ortogonali.
Sulla base di questo confronto si evince come i risultati derivanti dal modello di piastra ortotropa risultano più contenuti di quelli ricavati dal modello monodimensionale a causa dell’interazione dei due ordini di travi e a causa dei vincoli laterali, e si evidenzia come l’impiego del calcolo semplificato seppure sia accettabile porta a sovradimensionare i travetti di bordo, i quali a causa della presenza del vincolo esteso sono poco sollecitati. Comunque un’ulteriore considerazione che convalida l’utilizzo del modello di trave continua risiede nella possibile fessurazione della soletta nella zona di collegamento laterale (bordo destro e sinistro dell’esempio analizzato), infatti nel caso si dovesse creare la sconnessione tra il solaio e la trave, da imputare ad una differente deformazione dei due elementi, verrebbe a mancare la condizioni di vincolo laterale, riconducendo lo studio ad un elemento bidimensionale poggiato solo sui due lati ortogonali alle nervature. In questo caso le sollecitazioni ottenute dalle integrazioni sono per tutti i travetti uguali a quelle ricavate per il travetto 8, ossia quello disposto in mezzeria quindi la sovrastima delle sollecitazioni ottenute dal modello monodimensionale sarebbe assolutamente accettabile, circa il 25% sul momento e il 10% sul taglio. Perciò ragionando nello spirito che l’adozione di vincoli ridotti rispetto a quelli reali risulta sempre a favore di stabilità statica, è assolutamente accettabile, per il calcolo delle sollecitazioni, utilizzare il modello di trave continua su appoggi fissi. Infatti in questo modo si applica una notevole semplificazione nel calcolo, con la consapevolezza di avere una certa riserva di resistenza dettata dal comportamento di “piastra” della struttura.

Ing. Davide Cicchini
Clicca qui per scoprire il libro scritto dall’Ing. Davide Cicchini

Commenti

commenti